目录
1、回顾:实结构
2、微分流形
3、实例
4、切空间
5、子流形
6、弗洛贝尼乌斯定理(Frobenius' Theorem)
回顾:实结构
在开始进入流形的具体概念之前,我们先复习一遍分析和代数中关于实空间度量和拓扑的基本观点。
我们使用\(\R\)来表示实数域。令 \[ \R^m\;=\;\{\textbf x = (x^1,x^2,...,x^m)|x^i\in\R,\;1\le i\le m\} \] 这是m维实数元组的集合。数字\(x^i\)称为元素\(\textbf x \in \R^m\)的第i坐标分量。对于任意的\(x,y\in \R^m,a\in \R\),我们有 \[ (x+y)^i=x^i+y^i\\ (ax)^i=ax^i \] 这定义了集合\(\R^m\)中的加法和标量积,因而使得其成为一个R上的m维向量空间。
除了线性结构,\(\R^m\)也有标准拓扑结构。如定义 \[ d(x,y)=\sqrt{\sum^m_{i=1} (x^i-y^i)^2}\;\;\;\;\;\;,x,y\in \R^m \] 显见d为一度量。因而\((\R^m,d)\)为一度量空间。在\(\R^m\)上由d诱导出的拓扑便称为自然拓扑。因而其具有自然拓扑结构。配备有度量d的m维向量空间\(\R^m\)称为m维欧几里得空间(Euclidean Space)
设f是一个定义在m维欧几里得空间的某开子集U上的函数。如果对于一个正整数r,和任意的k\(\le\)r,f的k阶任意偏导数都存在且连续,那么我们说f属于U上的r阶连续可微类,记作\(f\in C^r(U)\)。如果对于任意正整数r都有\(f\in C^r(U)\),那么我们说f属于U上的光滑函数类,记作\(f\in C^\infin(U)\)。如果f是解析的,也就是说,如果f在属于U的每个点的某个邻域内都可以表示成幂级数,那么我们说f属于U上的解析函数类,记作\(f\in C^\omega(U)\)
以上基本概念相信我们已经非常熟悉了。下面介绍流形的定义和概念。
微分流形
要问微分几何研究的主要对象是什么,那必定是微分流形无疑。微分流形是建立在流形的基础上的,所以我们先来讲讲流形的概念。
流形是黎曼在研究微分几何时引入的概念,我们说一个集合是一个流形,大体上的意思是讲这个集合是有若干片欧几里得空间“拼接”而成。
定义1:流形
设M是豪斯多夫空间(Hausdorff Space),如果\(\forall p \in M,\exist U(p)是p的邻域\),使得U同胚于\(\R^m\)的某个开子集,那么我们说M是一个m维流形(manifold)或m维拓扑流形。
设上述定义中的同胚映射是\(\varphi_U:U\to\varphi_U(U)\),此处\(\varphi_U\)(U)是m维欧几里得空间中的开集。那么我们称\((U,\varphi_U)\)是M的一个坐标卡。由于\(\varphi_U\)是同胚,我们可以定义U中元素y的坐标为 \[ u^i = (\varphi_U(y))^i \;\;\;\;i=1,2,...,m \] 其中的u,我们称为y的本地坐标或局部坐标。
设\((U,\varphi_U),(V,\varphi_V)\)是两个坐标卡,如果U和V的交不空,那么\(\varphi_U(U\cap V)\)和\(\varphi_V(U\cap V)\)都是\(\R^m\)里的非空开集。映射$ _U_V^{-1} \(就是定义在\)_U(UV)\(上,到\)_V(UV)$的函数,易见该函数是双射,设它为f,其反函数为g,那么 \[ y=f(x)\\ x=g(y) \] 又有 \[ f(g(y))=y\\ g(f(x))=x \] 对于两个坐标卡\((U,\varphi_U)\),\((V,\varphi_V)\),我们说他们是\(C^r\)相容的,指的是要么\(U\cap V = \varnothing\), 要么f和g都是r次连续可微类(注意f和g都是实集上的函数,所以可微性是已经定义好的)。
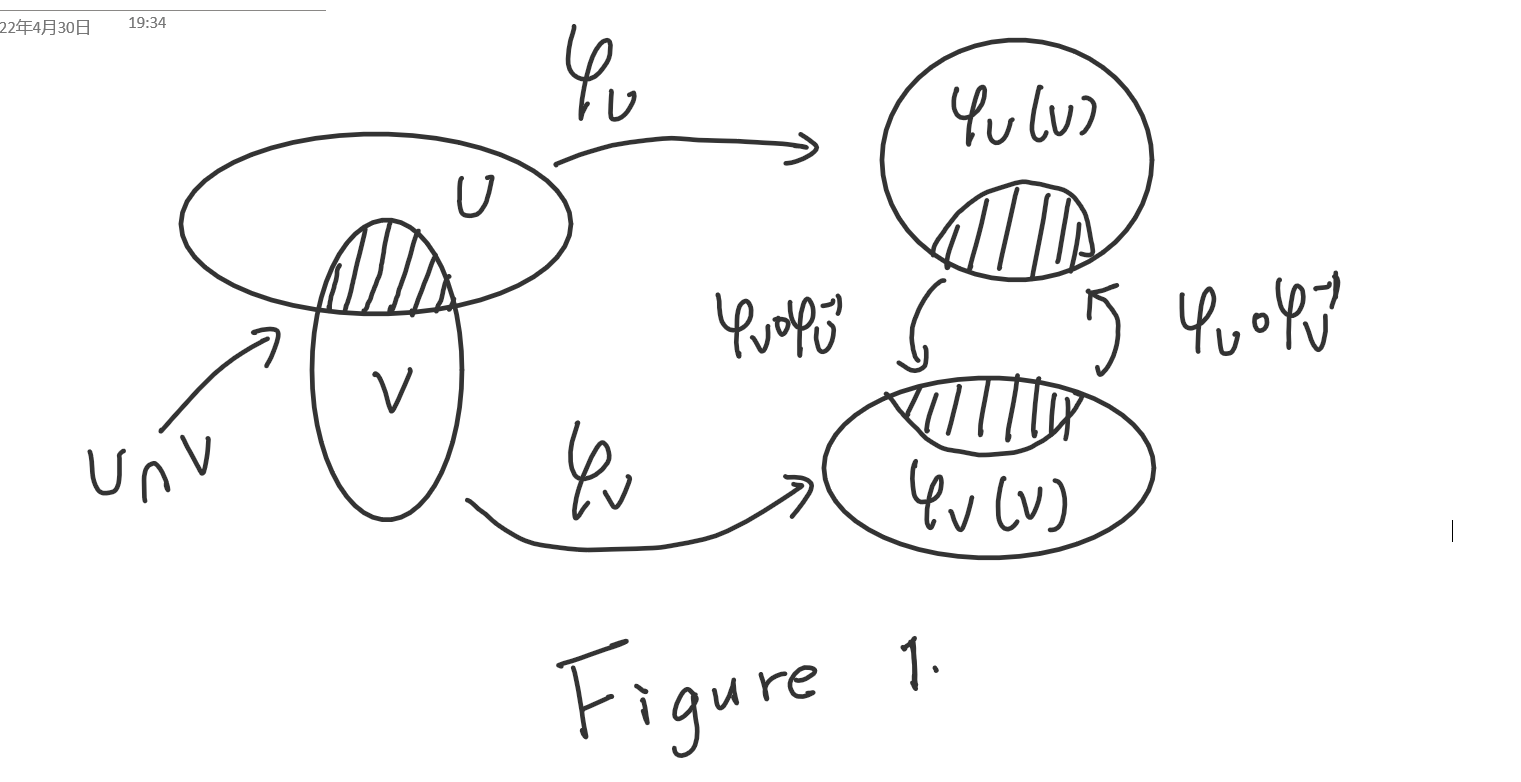
定义2:微分结构
设M是一个m维流形。如果对于一个M上的坐标卡集合\(\mathcal A\)满足以下条件,那么我们称\(\mathcal A\) 是一个M上的r次可微类微分结构(\(C^r\)-differentiable structure):
(1){U,V,W,...}是一个M上的开覆盖。
(2)任何两个坐标卡都是\(C^r\)相容的。
(3)\(\mathcal A\)是极大的。也就是说,任何一个坐标卡如果它于任何\(\mathcal A\) 中的坐标卡都\(C^r\)相容,那么它必属于\(\mathcal A\)。
具有r阶可微类微分结构的集合M叫做r次可微微分流形,其中的坐标卡叫做M的相容坐标卡。M中点p的局部坐标系统,从现在起将总是从包含p的相容坐标卡中作出的。
我们容易看出,微分流形结构中的前两条都是基本的。不难验证,如果一个坐标卡集\(\mathcal A'\)满足前两个条件,那么对于任意一个正整数s,\(0<s\le r\),都存在唯一一个s可微微分结构\(\mathcal A\),使得\(\mathcal A' \subset \mathcal A\)。这个微分结构\(\mathcal A\)是由\(\mathcal A'\) 唯一决定的。因此要产生一个r次微分结构,只需要指明一个相容的开覆盖坐标卡即可。
注:我们提及的流形M将总是假设为第二可数的。
如果在M上给定了一个\(\infin\)阶微分结构,那么我们称M为一个光滑流形。如果给定了一个\(C^\omega\)微分结构,那么我们称M为一个解析流形。我们最感兴趣的是光滑流形,因而当我们没有特意提及时,总是假定指定的流形是微分流形。
定义了流形和微分结构之后,我们还缺乏结构上或结构之间的联系,所以我们还需要定义流形上或流形之间函数的可微性和积流形的概念。
在光滑流形上,光滑函数的概念是良好定义的。注意到M上的函数f和局部坐标函数的反函数\(\varphi_U^{-1}\)的复合是一个从 \(\R^m\)到 \(\R^m\)的映射,而且对于任意其它的坐标卡\(\varphi_V\),总有\(f\circ \varphi_V^{-1} = f\circ \varphi_U^{-1} \circ (\varphi_U \circ \varphi_V^{-1})\),所以我们看出这个复合函数的可微性是和坐标卡选择无关的,因而可以找出f可微性和光滑性的定义。
实值光滑函数只不过是光滑流形间光滑函数的特例。
定义3:光滑函数
设\(f:M\to N\)是连续映射,其中M和N都是光滑流形。且dim(M)=m,dim(N)=n。如果在\(p\in M\)处存在相容坐标卡\((U,\varphi_U)\),且在f(p)处也存在相容坐标卡\((V,\varphi_V)\),使得映射 \[ \psi_V\circ f\circ \varphi_U^{-1}:\varphi_U(U)\to\psi_V(V) \] 在点\(\varphi_U(p)\)是光滑的,那么f在p点被叫做\(C^\infin\) 的。如果映射f在M上的每一点都是\(C^\infin\) 的,那么f被称为M上的光滑函数。
在m=n的情形下,如果f是一个同胚映射且\(f\)和\(f^{-1}\)都是光滑函数,那么f被称为一个微分同胚映射。如果M和N是微分同胚,那么我们说它们对应的光滑微分结构是同构的。稍后我们会见到,在米勒球的例子中,两个微分结构是同胚但不同构的。
另一个重要的例子是所谓的流形上的参数曲线。M是流形\((a,b)\subset R\),那么f:\(M\to N\)就是N上的一个参数曲线。
设M和N分别是m维和n维光滑流形,具有微分结构\(_{\alpha\in \mathcal A}\)和\({(V_\beta,\psi_\beta)_{\beta\in \mathcal B}}\)。显然我们可以构造一个(m+n)维的光滑流形\(M\times N\)通过将M和N“粘合”在一起。
首先看到\(\{U_\alpha\times V_\beta\}_{\alpha\in \mathcal A,\beta\in \mathcal B}\)是一个开覆盖。然后我们定义映射 \[ \varphi_\alpha \times \psi_\beta:U_\alpha \times V_\beta \to \R^{m+n} \;\;\;\;s.t.\\ \varphi_\alpha \times \psi_\beta (p,q)=(\varphi_\alpha(p),\psi_\beta(q)),\\ (p,q)\in U_\alpha \times V_\beta \] 容易验证\((U_\alpha \times V_\beta, \varphi_\alpha \times \psi_\beta)\)是一个坐标卡。容易验证它们都是\(C^\infin\)相容的,所以我们就构造出了一个新的光滑微分结构。
定义4:积流形
以上定义的新的微分结构下,\(M\times N\)称为由M和N产生的积流形。
其自然投影\(\pi_1:M\times N \to M\)和\(\pi_2:M \times N \to N\)都是光滑的。
实例
m维球面
m维球面是一个常见但却很丰富的结构。
考虑m维单位球面 \[
S^m = \{x\in R^{m+1}| \sum^{m+1}_{i=1}(x^i)^2=1 \}
\] 不妨先考虑m=1时的情形。此时,取如下四个坐标卡: \[
U_1=\{x\in S^1|x^2>0\},\varphi_{U_1}(x)=x^1\\
U_2=\{x\in S^1|x^2<0\},\varphi_{U_2}(x)=x^1\\
V_1=\{x\in S^1|x^1>0\},\varphi_{V_1}(x)=x^2\\
V_2=\{x\in S^1|x^1<0\},\varphi_{V_2}(x)=x^2
\] 显然,\(\{U_1,U_2,V_1,V_2\}\)是\(S^1\)的一个开覆盖。在交集\(U_1 \cap V_2\)中,我们有 \[
\begin{cases}
x^2 = \sqrt{1-(x^1)^2}\;>0\\
x^1 = -\sqrt{1-(x^2)^2}\;<0
\end{cases}
\] 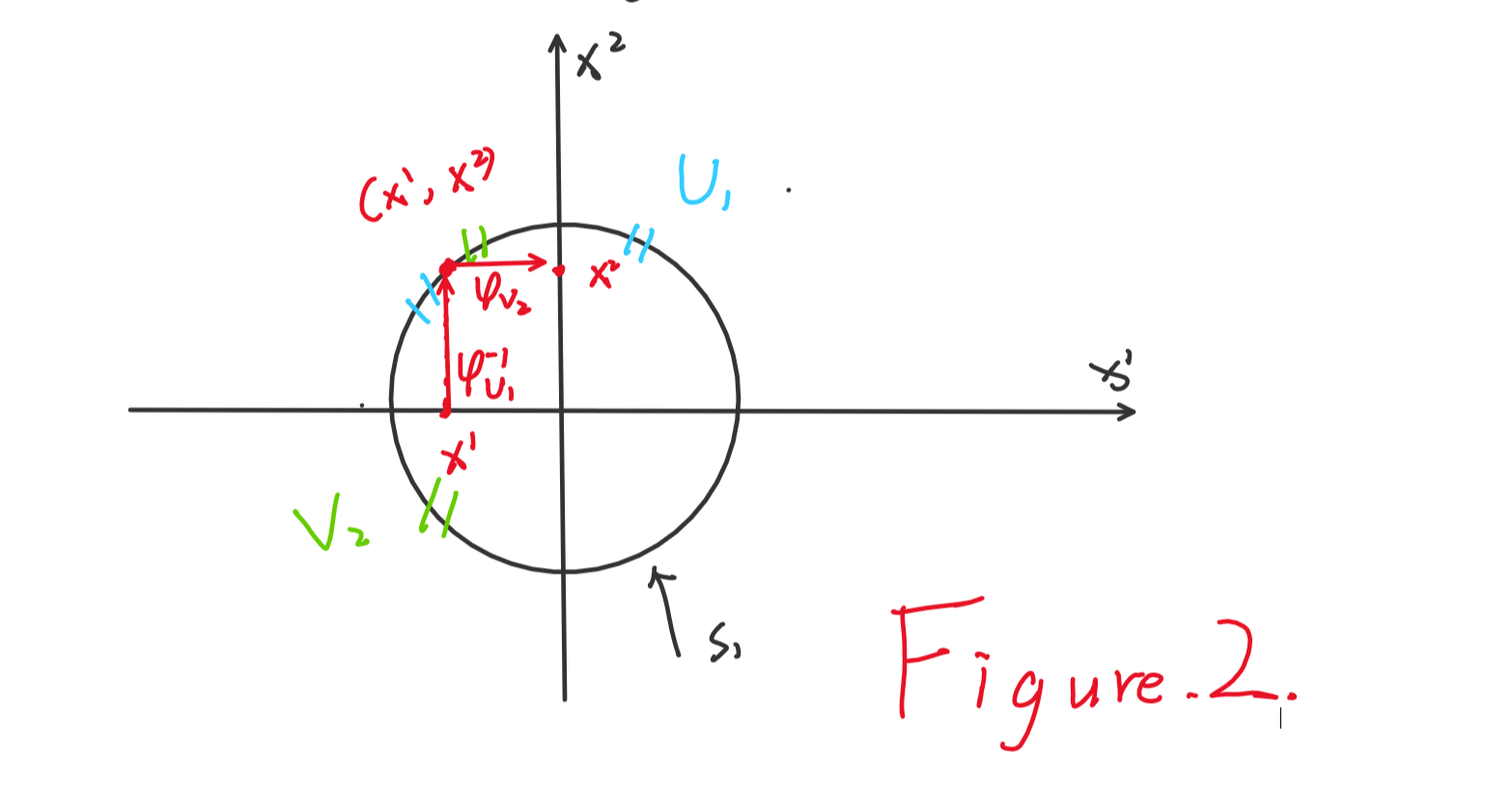
可见二者都是\(C^\infin\)的,因而这两个坐标卡是\(C^\infin\) 相容的。类似的,其它坐标卡之间的关系也可以类似作出。因而我们断定,这些坐标卡组成的微分结构使得\(S^1\)成为一个一维光滑流形。m>1时的微分结构可以类似得出,留给大家自证。
m维射影空间(\(P_m\))
射影空间是我们已经在代数和几何中熟知的空间。我们来分析m维射影空间\(P_m\)的微分结构。
在\(\R^{m+1}-{0}\)中定义关系\(\sim\),使\(x\sim y\)当且仅当存在一个实数a使得x=ay。容易看出来,\(\sim\)是一个等价关系。记x的等价类为\([x]=[x^i]\),那么m维射影空间定义为 \[ \begin{align} P_m&=(\R^{m+1}-\{0\})/\sim\\ &=\{[x]|x\in \R^{m+1}-\{0\}\} \end{align} \] \((x^i)\)这个m+1维元组被称为[x]的齐次坐标。它们被[x]中的一个非零向量决定。所以m维射影空间\(P_m\)实质上是\(\R^{m+1}\)中过原点的直线的集合。
接下来我们构造\(P_m\)上的微分结构。令 \[
\begin{align}
\begin{cases}
U_i&=\{[x^1,...,x^m+1]|x^i\ne 0\}\\
\varphi_i([x])&=(_i\xi_1,_i\xi_2,...,_i\xi_{i-1},_i\xi_{i+1},...,_i\xi_{m+1})
\end{cases}
\end{align}
\] 其中\(_i\xi_j =
x_j/x_i\)。容易看出,\(U_i\)是\(P_m\)的一个开覆盖,在\(U_i \cap U_j\)上,坐标变换表示为 \[
\begin{cases}
_j\xi_h = \frac{_i\xi_h}{_i\xi_j},h\ne i,j;\\
_j\xi_i = \frac{1}{_i\xi_j}
\end{cases}
\] 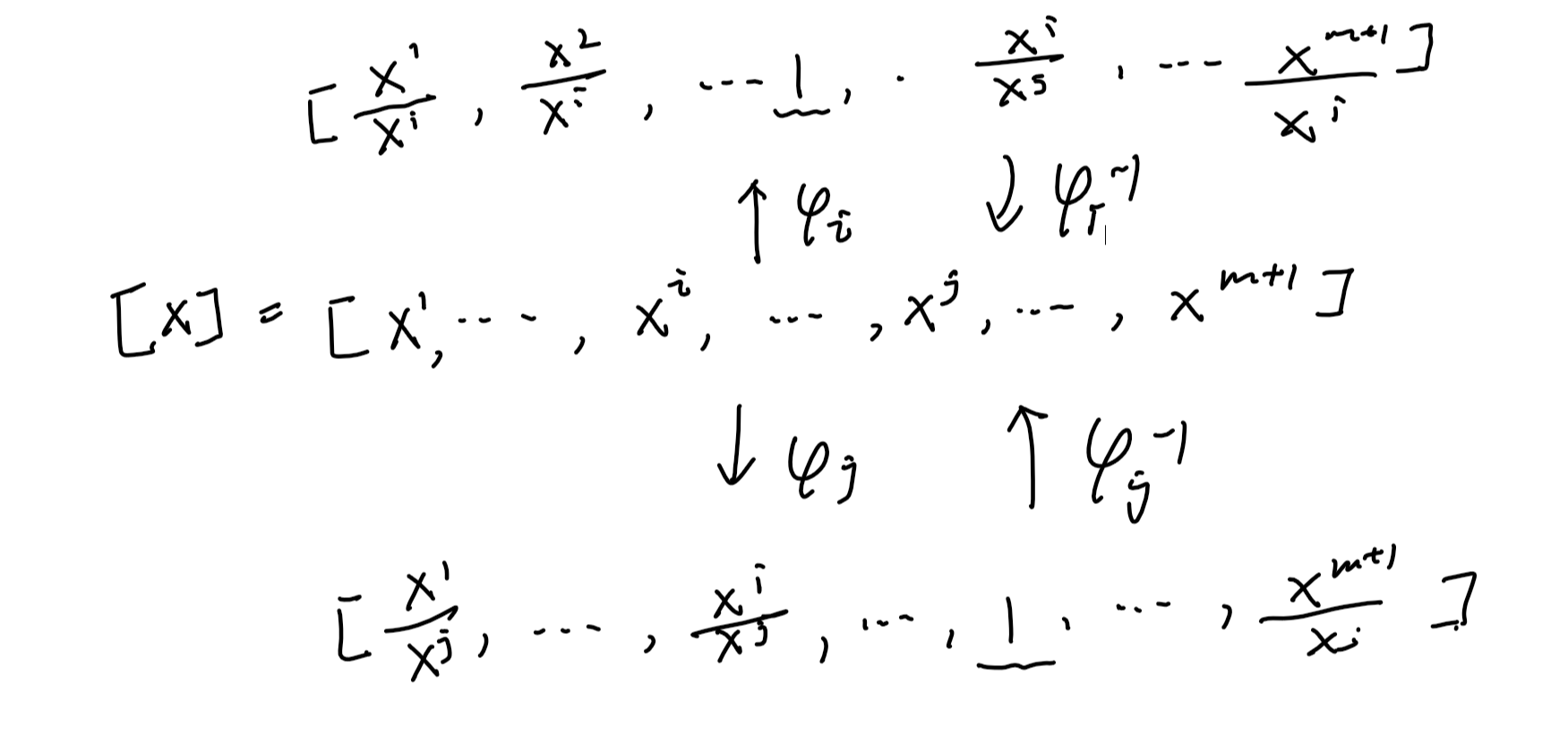
容易验证,这是一个\(P_m\)上的光滑微分结构。
米尔诺球(Milnor's Sphere)
切空间
引入:光滑函数芽上的等价类
在一个正则曲线(或曲面)上的任何一个点我们都可以指出切线(或是切平面)的概念。与之类似,在拓扑流形上给定一个微分结构,我们可以用一个线性空间近似任何一点的邻域。更准确的说,我们将使用切空间和余切空间。
设M是一个m维光滑流形。给定一个点\(p\in M\) ,设f在p的一个邻域内是光滑的。我们将所有的这些函数的集合记作\(C^\infin_p\) 。自然,其中任意两个函数的定义域都可能是不同的,但是在其中的函数的加法和乘法运算依旧是良好定义的,只需将结果函数的定义域限制在两函数的定义域的交集上去即可。
在如上的集合中定义一个关系\(\sim\) 如下:设\(f,g\in C^\infin_p, then\; f \sim g\;\;\iff\;\; \exist H(p) \;s.t.\; f|_H = g|_H\)。显然\(\sim\) 是一个等价关系。按照这个等价关系划分\(C^\infin_p\) 等价类[f],这个商空间就叫做p点处的光滑函数芽。即: \[ \mathcal F_p=C^\infin_p/\sim=\{[f]|f\in C^\infin_p\} \] 可以定义函数芽中的加法和标量积运算,从而使得该光滑函数芽成为\(\R\)上的线性空间。大家自行验证其为无穷维线性空间。
设\(\gamma\) 是M上过点p的参数曲线。\(i.e. \exist \delta>0,\;s.t.\;\gamma:(-\delta,\delta)\to M\)是一个光滑映射同时\(\gamma (0)=p\)。将所有这样的参数曲线的集合记为\(\Gamma_p\)。
对于任意的\(\gamma \in \Gamma_p\) 和 \([f]\in \mathcal F_p\),令 \[ <<\gamma, [f]>>\;=\;\frac{\mathrm d (f\circ \gamma)}{\mathrm d t}|_{t=0},\;\;-\delta<t<\delta \] 容易看出,上式对于给定的\(\gamma\) ,其值只取决于对于等价类[f]的选取。同时算符<<,>>对于第二变元也是线性的。
令 \[ \mathcal H_p = \{[f]\in \mathcal F_p|<<\gamma,[f]>>=0,\forall \gamma\in \Gamma_p\} \] 容易验证\(\mathcal H_p\)是\(\mathcal F_p\)的线性子空间。
定理1
\[ 设[f]\in \mathcal F_p,对于容许坐标卡(U,\varphi_U)令:\\ F(x^1,...,x^m)=f\circ \varphi_U^{-1}(x^1,...,x^m)\\ 那么[f]\in\mathcal H_p \iff\frac{\partial F}{\partial x^i}|_{\varphi_U(p)} = 0\;\;,1\le i\le m \]
使用本地坐标表示,直接求导易证。
这个定理表明,\(\mathcal H_p\) 中的元素实际上都是那些在局部坐标系中的p点的所有偏导数都为0 的函数类组成。
接着我们进入余切空间和切空间的表示。
余切空间与切空间
定义1:余切空间
\[ 商空间\mathcal F_p/\mathcal H_p叫做M上p点的余切空间,记作T^*_p(或T^*_p(M)).\\\mathcal H_p中的函数芽[f]的等价类被记作\tilde {[f]}(或(df)_p),被称为M上p点的余切向量. \]
容易看到,余切空间也是线性空间。
我们已经离完整描述相当接近了,接下来给出链法则。
定理2:链法则
\[ 设f^1,f^2,...,f^m\in C^\infty_p,F(y^1,...,y^m)是点f_p的邻域内的光滑函数,其中f_p = (f^1(p),f^2(p),...,f^m(p)),\\ 那么f=F(f^1,f^2,...,f^m)\in \R^m,且(df)_p=\sum^m_{i=1}[(\frac{\partial F}{\partial f^i}(f^1(p),f^2(p),...,f^m(p)))\; \dot \;(df^i)_p] \]
证明较为直接,只要注意\((df)_p = (dg)_p \iff [f]-[g] \in \mathcal H_p\)即可。
该定理给出的形式近似于我们在多元微分学中看到的链式法则,我们会在后面的学习中看到两者形式间的关系。
根据此定理,我们可以较为方便的计算出一些余切向量间的关系,例如 \[ d(fg)_p = f(p)\dot\;(dg)_p+g(p)\dot\;(df)_p \] 而且我们可以得出推论,余切空间是一个m维向量空间。
推论:dim \(T^*_p\) = m
要证明这个结论,只要选定局部坐标系,证明一组自然坐标是余切空间线性无关的基底即可。读者自证不难。
定义了余切矢量和余切空间之后,我们注意到,上面定义的算符<<,>>的第一变元,即参数曲线,也可以进行与余切情形对偶的讨论。
首先,根据定义\([f]-[g] \in \mathcal H_p \iff <<\gamma,[f]>> = <<\gamma,[g]>>\)因而可以定义余切矢量在该算符下和它所代表的等价类中的一个相同:\(<<\gamma,(df)_p>>=<<\gamma,[f]>>\)。
然后,定义参数曲线的等价关系\(\sim in\; \Gamma_p\)。假设\(\gamma,\gamma' \in\Gamma_p\)。那么\(\gamma \sim\gamma'\iff\;\forall(df)_p\in T^*_p,<<\gamma,(df)_p>> = <<\gamma',(df)_p>>.\)
显然这是个等价关系。记等价类为\([\gamma]\),那么我们可以定义\(<[\gamma],(df)_p>=<<\gamma,(df)_p>>\).我们将证明\(\gamma\)的等价类恰可以构成余切空间的对偶空间。
借用前面的记号,我们有 \[ <[\gamma],(df)_p>=\sum^m_{i=1}a_i\xi^i,in\;\;which\\ a_i =(\frac{\partial (f\circ \varphi^{-1}_U)}{\partial u^i})_{\varphi_U(p)},\xi^i =(\frac{du^i}{dt}) \] 我们发现,这时\(a_i\)不过是余切矢量\((df)_p\)在自然基底\((du^i)_p\)下的分量。显然\(<[\gamma],(df)_p>\)是一个余切空间中的线性函数(想想内积),而且这个函数受\(\xi^i\)唯一决定。那么我们可以选择\(\gamma\),使得\(u^i(t) = u^i(p)+\xi^it\)。\(\xi^i\)是任意的。可以看出来此时这个算符可以表达出来所有余切空间中的线性函数了。我们称这样的所有函数构成的空间为切空间,它的元素称为切矢量。它是余切空间的对偶空间。
上面从分析的角度确定了切向量的表示,那么它到底有什么几何含义呢?其实这是相当清楚的,我们只要看到什么情况下参数曲线的等价类相等就好。根据我们上面的定义,因为\((df)_p\)是任意的,所以如果\(\gamma,\gamma'\in\Gamma_p\; is\; given \;by\;u^i = {u'}^i(t),\;\;1\le i\le m\),那么 \[ [\gamma]=[\gamma']\iff(\frac{du^i}{dt})_{t=0}=(\frac{d{u'}^i}{dt})_{t=0} \] 这个等式不过是说,所有在p点导数取得相同的值的曲线同属一个等价类,也就是说,一个切向量表示的是所有在p点具有相同切向量的曲线的集合。
通过上面的一系列讨论我们可以对切空间和余切空间有一个基本的认识了,首先 \[ <X,(df)_p>,\;\;\;X=[\gamma]\in T_p,(df)_p\in T^*_p \] 是双线性的。
我们这样选取参数曲线,使得\(u^i\circ \lambda_k = u^i(p)+\delta^i_kt\),那么显然\(<[\lambda_k],(du^i)_p>=\delta^i_k\),容易验证我们这样选取的\([\lambda_k]\)就是基底ui的对偶基底。
我们从另一个角度看这组基底,用一个任意的余切矢量试探,看二者会发生什么: \[ \begin{aligned} <[\lambda_k],(df)_p>=&<[\lambda_k],\sum^m_{i=1}(\frac{\partial f}{\partial u^i})_p \cdot (du^i)_p>\\ =&(\frac{\partial f}{\partial u^k})_p \end{aligned} \] 仍然记得这里的偏导数总是在局部坐标系下进行的,将\(f\circ \varphi^{-1}_U\)记成了\(f\),所以是有意义的。这个等式直接给出了一个让我们熟悉的偏导数关系。我们认定,\([\lambda _k]\)就是在函数芽\([f]\)上的偏微分算符。两组基底之间的关系也可以重新写为 \[ <\frac{\partial}{\partial u^k}|_p,(df)_p>=\delta^i_k \] 从这里开始,我们把余切空间的自然基底ui的对偶基底叫做切空间的自然基底,从我们定义的过程来看,任何一个位于切空间中的等价类\([\gamma]\)都可以写成 \[ [\gamma]=\sum^m_{i=1}\xi^i\frac{\partial}{\partial u^i}|_p \] 式中\(\xi^i\)为切矢量的分量。根据基底关系,任何一个切矢量均由这样的分量唯一确定。两个切矢量的和以及数乘都可以看做是对于这样的分量的运算。
从这里开始,我们在不引起混淆的情况下将省略表示该点 的下标p。
下面我们要将切矢量和余切矢量和我们已有 的知识形式建立联系。
定义2:微分
\[ 设f是一个定义在点p附近的光滑函数.那么(df)_p\in T^*_p也被叫做f在p点的微分.如果(df)_p=0,那么p叫做f的一个临界点(Critical Point). \]
函数的临界点一般包含着关于函数的很多信息,因而很值得研究。关于函数的临界点的研究有一个专门分支叫做Morse理论,有兴趣我会顺便讲一讲。
定义3:方向导数
\[ 设X\in T_p,f\in C^\infty_p.记Xf=<X,(df)_p>.Xf叫做f沿着向量X的方向导数. \]
我们立刻可以得到一些关于方向导数的计算法则:
定理3:方向导数的运算
\[ X(\alpha f+\beta g)=\alpha \cdot Xf+\beta\cdot Xf\\ X(fg)=f(p)\cdot Xg+g(p)\cdot Xf \]
注:第一条性质就是线性性质,第二条性质就是所谓的积函数求导法则。这些结论都是自然的,取f=g=1,我们可以简单的看到,在常函数上应用方向导数得到0.
注:在其它微分几何的教材中我们经常看到,以上两条性质常常被用来定义切矢量(而不是像我们从切矢量的另一部分导出)。这不过是从两个角度出发来探讨切矢量的性质。事实上,任何在p处光滑函数芽上满足这两条性质的函子形成余切空间的对偶空间,而且必然和切空间相同。
接下来我们将讨论不同本地坐标下的基底变换(latex救我😭😭😭)。
---待续---
